Lösung:
Kubisch
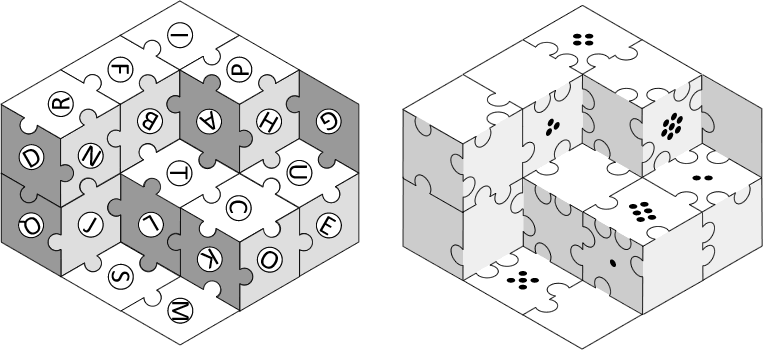
Für Akt 1 muss man einfach die Rauten passend zusammensetzen. Der Rahmen weißt darauf hin, dass die Farbe der Raute die Orientierung bestimmt.
Der Vergleich von Akt 1 und Akt 2 lässt erkennen: Es sind gleich viele Teile. Mehr noch: Gleich viele Ecken, gleich viele Kanten und gleich viele Innenteile. Das ist natürlich kein Zufall. Allerdings haben wir Quadrate, keine Rauten. Hier hilft ein Perspektivenwechsel:
Das Ergebnis von Akt 1 lässt sich nämlich auch als eine dreidimensionale Konstellation von Würfel interpretieren. Und die Seitenflächen lassen sich nun mit den Teilen von Akt 2 wunderbar auslegen.
Praktisch gesehen muss man ein bisschen tolerant sein (egal ob im Onlinetool, oder mit ausgedruckten Teilen), aber das könnte ungefähr so aussehen (ich habe dafür extra z10 gebeten, auch in Akt 2 die Teiledrehung in 30° Schritten zu ermöglichen):

Am Ende vergleicht man einfach die markierten Teile des zweiten Akts mit den Buchstaben der dazugehörigen Teile des ersten Akts. Heraus kommt: KUBISCH
Der halbe Akt ist recht geradlinig: Hier handelt es sich um den Baconcode. Einerseits über die Noppenrichtung Zeilen/Spaltenweise: So ist die erste Zeile (rechts-links-links-rechts-rechts) als BAABB=V zu interpretieren, die zweite ergibt dann (links-links-rechts-links-links) AABAA=E usw. so geht man dann abwechselnd Zeilen und Spalten durch und erhaltet:
VERGLEICHE DIE TEILE AUS DEN BEIDEN AKTEN EINS UND ZWEI--
Andererseits kann man auch die Richtung der Noppen ignorieren und stattdessen die Größe beachten.
Die erste Zeile (klein-klein-klein-klein-groß) ist dann als AAAAB=B zu interpretieren.
Hier erhaltet man:
BUCHSTABEN VORERST UNWICHTIG. FARBE ZEIGT AUSRICHTUNG-